Sorted by


Refresh


Filtered by

Automaton Type

Select / Deselect All














State Size

Select / Deselect All






Formula Length

Select / Deselect All






Temporal Hierarchy

Select / Deselect All








Spec Patterns

Select / Deselect All











Refresh


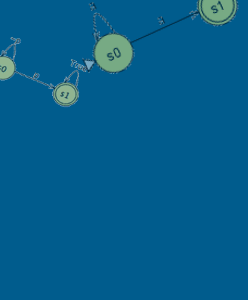
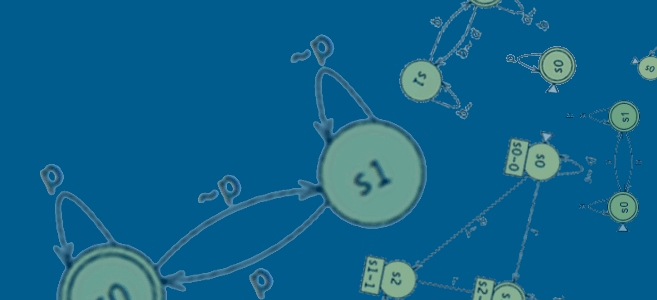
Grouped By


Refresh

View the filtered language classes in the "Containment Lattice"
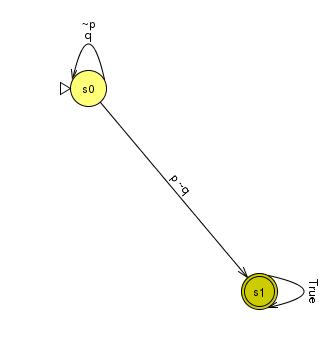
¬ G (p → ¬ p U q) Equivalent: ¬ G (p → ¬ p U q)
Complement:
DBW
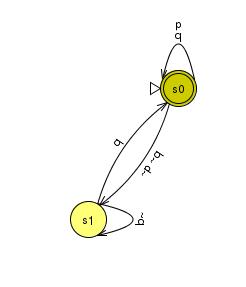
G (p ∨ F q) Equivalent: G (p ∨ F q)
Complement:
DBW
G p U ¬ p Equivalent: G p U ¬ p
Complement:
NBW
G (p ∨ ¬ O q) Equivalent: G (p ∨ ¬ O q)
Complement:
NBW
G (a ∨ ¬ X b) Equivalent: G (a ∨ ¬ X b)
Complement:
NBW
G F (p → q) Equivalent: G F (p → q)
Complement:
DBW
G (p ∧ F q) Equivalent: G (p ∧ F q)
Complement:
NBW
G ¬ p ∧ F q Equivalent: G ¬ p ∧ F q
Complement:
NBW
G F (¬ p ∧ ¬ q) Equivalent: G F (¬ p ∧ ¬ q)
Complement:
DBW
G F (¬ p ∨ q) Equivalent: G F (¬ p ∨ q)
Complement:
DBW
G ¬ p ∧ F ¬ q Equivalent: G ¬ p ∧ F ¬ q
Complement:
NBW
G (¬ p ∧ F ¬ q) Equivalent: G (¬ p ∧ F ¬ q)
Complement:
NBW
G F (p ∧ q) Equivalent: G F (p ∧ q)
Complement:
DBW
G (¬ p → F ¬ q) Equivalent: G (¬ p → F ¬ q)
Complement:
DBW
G (¬ p → X q) Equivalent: G (¬ p → X q)
Complement:
NBW