The main features of Büchi Store are grouped into 6 pages, namely
Search, Browse, Shopping Cart,
Upload, Settings, and Help.
In the following, we explain the functions provided in these pages, except
Help which leads to this page.
In addition, some use cases and public APIs for accessing the Store are
described at the end.
Search
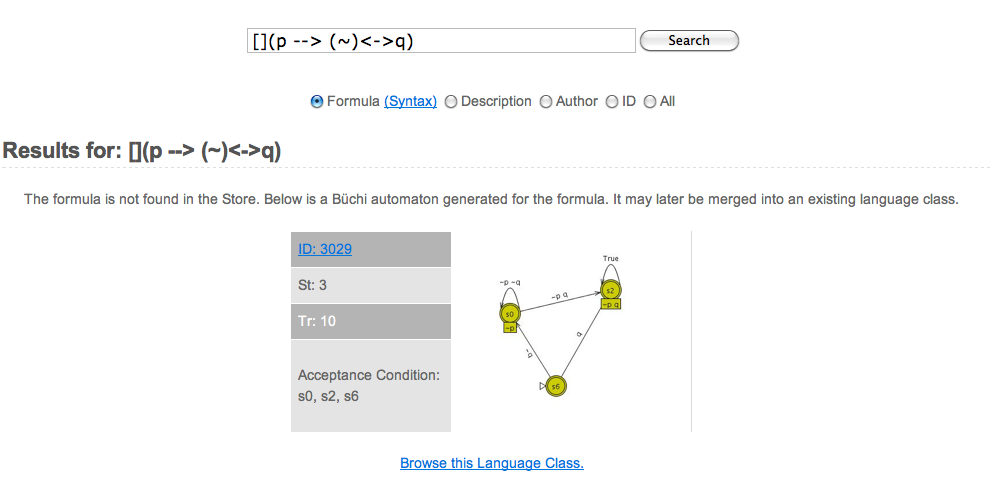
In the Search page, the search bar can be used to search for
automata that are equivalent to a specified formula.
Automata can also be searched by specifying a string for their descriptions,
an author, or an automaton ID.
The syntax of temporal formulae can be found in
this page.
Suggestions of Search Terms
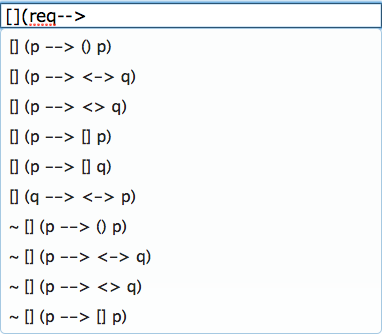
When a formula is partially entered in the search bar, a drop-down menu will appear with suggestions of possibly matched formulae (up to propositions renaming) in the Store. For example, suppose the user wants to search for a formula "[](req--><>ack)" (or equivalently "G (req --> F ack)". The following figure shows the suggestions when only "[](req-->" is entered in the search bar.
Note that only the first ten possibly matched formulae are listed as suggestions.
Search Results
The search results are automata that match the search term. For each automaton, its automaton ID, author, automaton type, equivalent formulae, and complement formulae will be shown on the screen.
When the user clicks on the automaton or a formula, the Store will display the equivalence class of the automaton or the formula. Please see the Equivalence Class section for more details.
Automatic Translation
If the formula is not found, the Store will translate the formula using various translation algorithms, simplify the results based on direct, reverse, and fair simulation relations, and return the smallest automaton obtained to the user.
Depending on the positions of quantifiers and temporal operators in a formula, different translation algorithms are applied. The translation algorithms applied in the automatic translation are shown in the following table where PNF indicates that the formula can be converted to prenex normal form, Future indicates that the formula does not contain any past operator, and Past indicates that the formula contains some past operators.
| Future | Past | |
|---|---|---|
| PNF | LTL2BA, Couvreur, LTL2BUCHI | LTL2AUT+, PLTL2BA |
| Not PNF | KP02 | |
Browse
This page provides various ways to browse automata in the Store.
The automata can be sorted according to a specified order, filtered based on
specified rules, and grouped by language classes.
By default, automata and formulae that are equivalent will be grouped
into an equivalence class and displayed as a single entry.
In this case, only the smallest automaton and the shortest formula in the
equivalence class are used as representatives of the equivalence class in
sorting and filtering.
Once the sort order and filter rules are decided, the user can click on the
Refresh button to browse in the specified order automata and
formulae that satisfy the specified filter rules.
“Containment Lattice” is another view of automata. In “Containment Lattice”, we focus on the containment relation among a finite set of selected language classes. Since the selected language classes do not form the whole ω-regular languages, “Containment Lattice” is formally not a lattice.
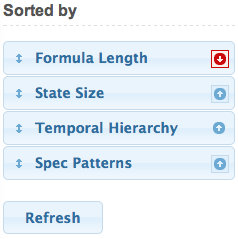
Sort
The automata can be sorted by four sort keys: state size, length of the shortest equivalent formula, class in the Temporal Hierarchy, and specification pattern. Note that in the Store, the formula length means the number of temporal operators. The priority of sort keys is decided by the order of the sort keys (from top to bottom); an upper sort key has a higher priority. The user may drag and drop sort keys to change their priorities. To change the order of a sort key, either ascending or descending, the user simply clicks on the sort key. The ascending order is displayed as an upward arrow, while the descending order is displayed as a downward arrow. For example, with the following criteria, the automata will be sorted first by formula length in a descending order, automata having equivalent formulae of the same length will be sorted by state size in an ascending order, and so on.
To make the new order effective, the user has to click on the
Refresh button.
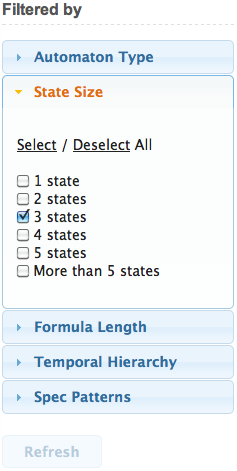
Filter
The automata to be displayed in the Browse page can be filtered
based on the automaton type, state size, length of the shortest equivalent
formula, class in the Temporal Hierarchy, and specification pattern.
When the automata are grouped by equivalence classes, an equivalence class
satisfies the filter rules if the rules are satisfied by the smallest
automaton and the shortest formula in the equivalence class.
To see the rules available in a filter, the user can click on the filter to
expand it.
Below is a filter example where only automata of 3 states will be displayed.
To make the new filter rules effective, the user has to click on the
Refresh button.
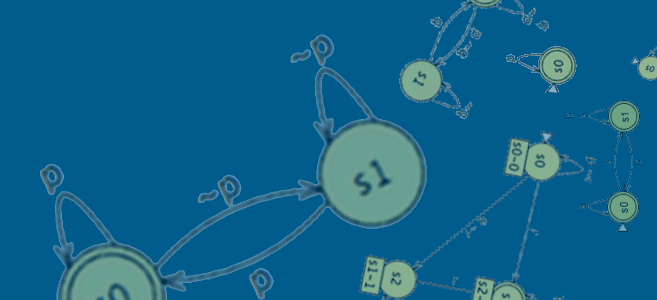
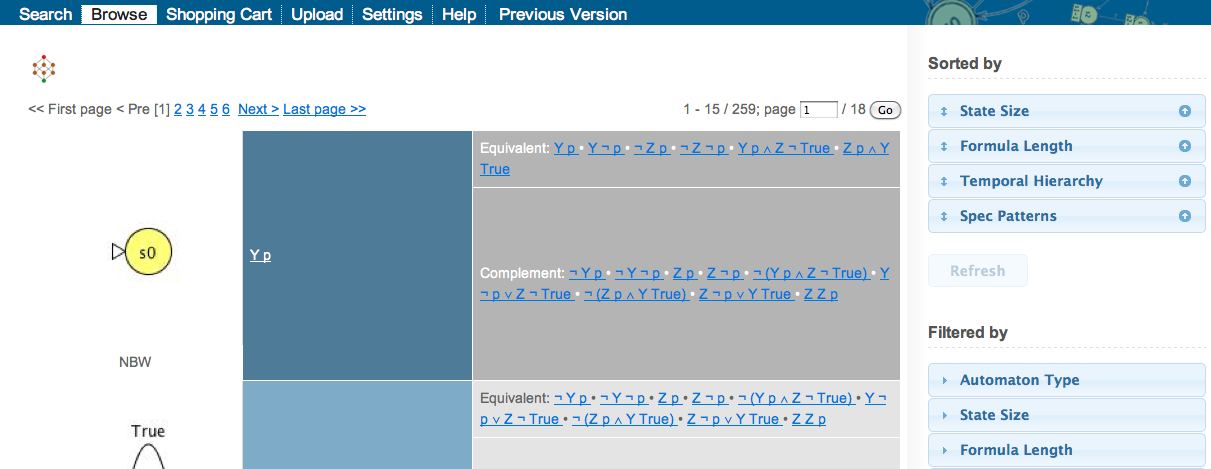
Equivalence Class
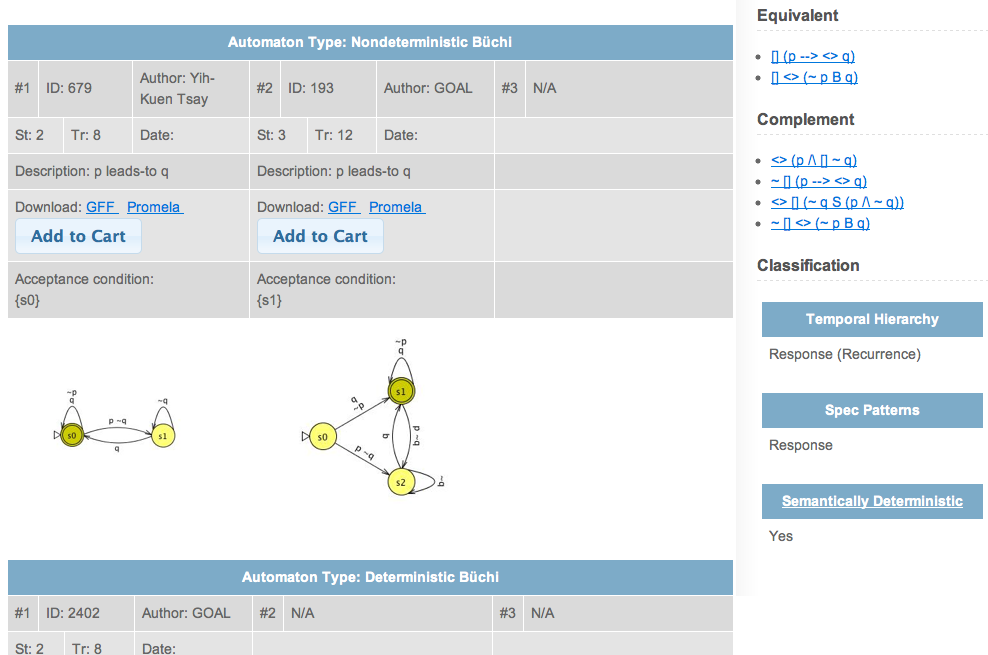
When the user clicks on an automaton or a formula, the Store will display the equivalence class of the automaton or the formula, as shown below.
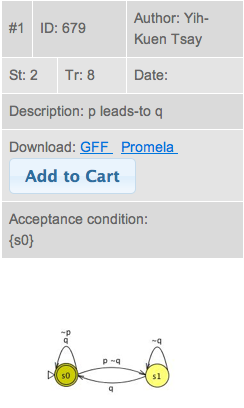
In this view, various types of equivalent automata are displayed on the left-hand side. For each automaton, the following properties are displayed:
- #: the rank of the automaton.
- ID: the unique ID of the automaton.
- Author: the author of the automaton.
- St: the number of states.
- Tr: the number of transitions. Note that the automaton is displayed with transitions simplified. For example, if there are two transitions labeled by "p q" and "p ~q" respectively from a state to another state in an automaton with the alphabet {p q, p ~q, ~p q, ~p ~q}, the two transitions will be displayed as a single transition labeled by "p".
- Date: the date when the automaton was uploaded.
- Description: the description of the automaton.
- Download: download links of the automaton in various formats.
The right-hand side of this page contains:
-
the equivalent formulae of the equivalence class in the
Equivalentsection, -
the complement formulae of the equivalence class in the
Complementsection, -
the classification of the equivalence class into the Temporal Hierarchy
and specification patterns in the
Classificationsection, and - a Yes/No indicating if the equivalence class is semantically deterministic, that is, equivalent to some deterministic Büchi automaton.
For each automaton, the user can click on the GFF link or the Promela link to
download the automaton in GFF (GOAL File Format) or in Promela.
The user can also click on the Add to Cart button to add both
the GFF file and the Promela file to the shopping cart.
When the user clicks on the Add to Cart button, the webpage will
switch to the Shopping Cart page.
If the user wants to download more automata, she/he can go back to the
previous page or browse the automata again and come back to the shopping cart
later.
Containment Lattice
This view focuses on the containment relation among a finite set of selected language classes. To view “Containment Lattice”, the user can click on one of the following two icons.
 :
This icon is located in the browse page.
It opens “Containment Lattice” to view the filtered
language classes.
:
This icon is located in the browse page.
It opens “Containment Lattice” to view the filtered
language classes.
 :
This icon is located in the view of a single equivalence class.
It allows the user to view the language class, its ancestors, and its
descendants in “Containment Lattice”.
:
This icon is located in the view of a single equivalence class.
It allows the user to view the language class, its ancestors, and its
descendants in “Containment Lattice”.
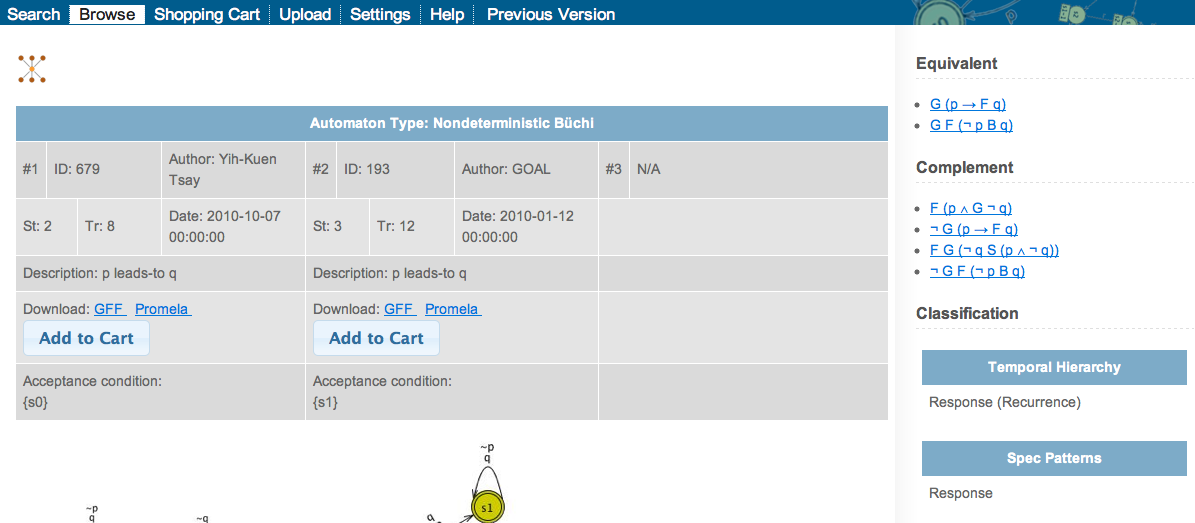
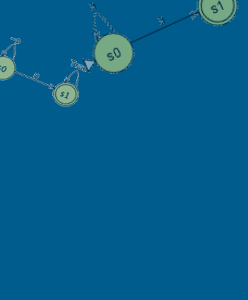
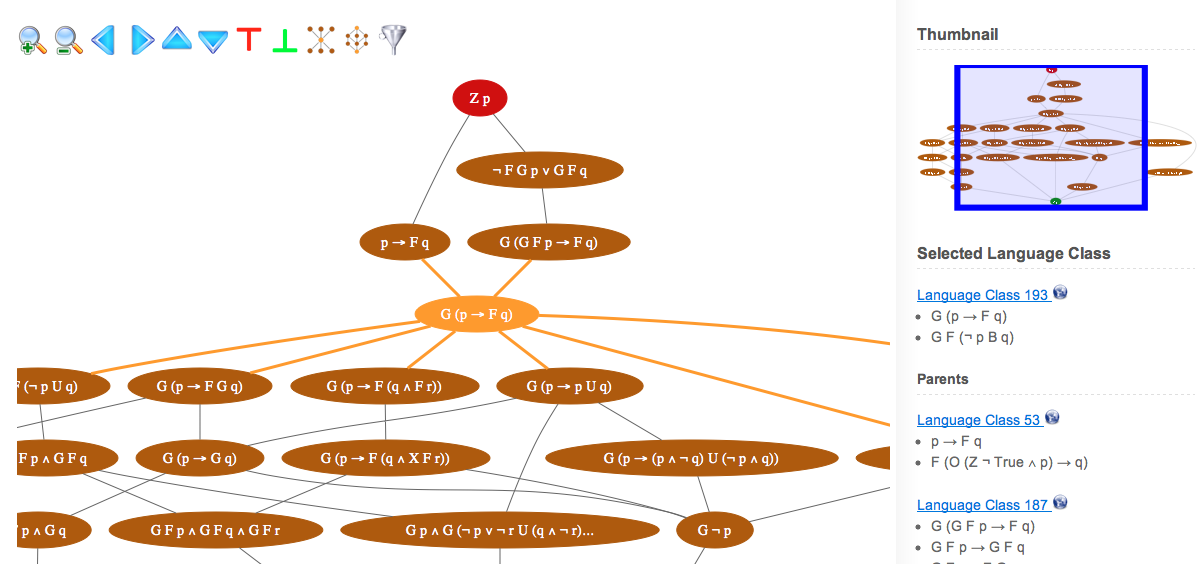
Below is a screenshot showing the language class equivalent to G (p → F q), its
ancestors, and its descendants in “Containment Lattice”.
Each language class is represented as an ellipse node.
The node label is a representative formula in the language class.
When the user clicks on a node, the node and its edges will be highlighted.
At the same time, formulae of the node, its parents, and its children will be displayed
in the right column.
If the user clicks on ![]() right of a language class in the right column, detailed information of the language class
will be displayed in a new window.
right of a language class in the right column, detailed information of the language class
will be displayed in a new window.
At the upper-left corner, there are several tool icons as described below.
-
 :
Zoom in.
:
Zoom in.
-
 :
Zoom out.
:
Zoom out.
-
 :
Move the view left.
:
Move the view left.
-
 :
Move the view right.
:
Move the view right.
-
 :
Move the view up.
:
Move the view up.
-
 :
Move the view down.
:
Move the view down.
-
 :
Highlight top.
:
Highlight top.
-
 :
Highlight bottom.
:
Highlight bottom.
-
 :
Display a selected language class, its ancestors up a specified level, and its
descendants down to a specified level in “Containment Lattice”.
Note that top and bottom will always be included.
:
Display a selected language class, its ancestors up a specified level, and its
descendants down to a specified level in “Containment Lattice”.
Note that top and bottom will always be included.
-
 :
Display all paths between two selected language classes.
Note that top and bottom will always be included.
:
Display all paths between two selected language classes.
Note that top and bottom will always be included.
-
 :
Change the filter rules.
A language class will not be displayed if it does not satisfy the filter rules.
:
Change the filter rules.
A language class will not be displayed if it does not satisfy the filter rules.
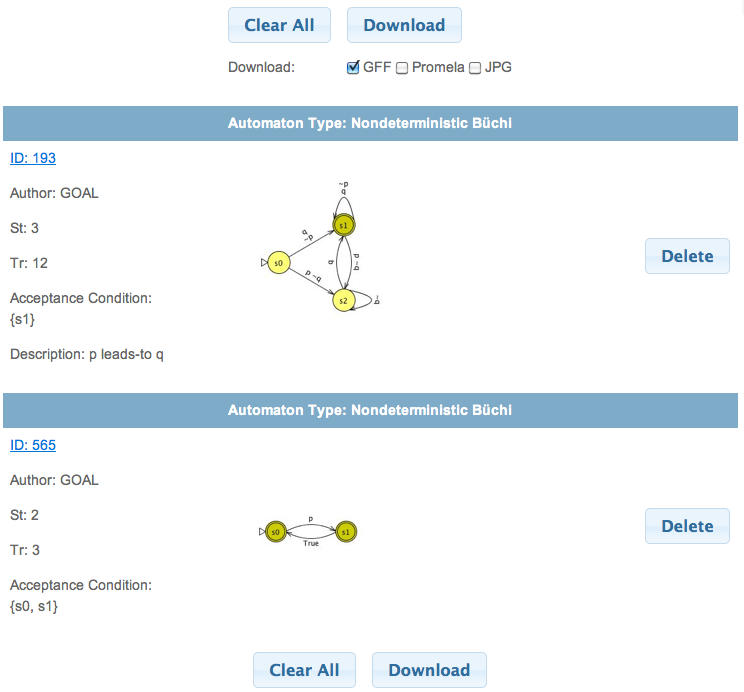
Shopping Cart
In the Shopping Cart page, the user can remove automata from
the shopping cart or download all automata in various file formats.
The Delete button can be used to remove a single automaton
while the Clear All button can clear the shopping cart.
When the user clicks on the Download button, a zip file
containing all the automata in the shopping cart will be downloaded.
Upload
In the Upload page, the user can contribute automata to the
Store.
The automaton file to be uploaded must be recognized by
GOAL.
Below is a list of file formats supported in GOAL for automata with
propositional alphabets.
- GFF (GOAL File Format) - the main file format in GOAL.
-
Promela Never Claim - the file format used by
Spin.
The Promela never claim may be output by
Spin, by
LTL2Buchi
with the
-o promelaargument, by MoDeLLa with the-sargument, or by other tools. -
LTL2Buchi Format - the XML file format output by
LTL2Buchi
with the argument
-o xml.
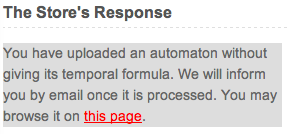
If the user does not provide an equivalent formula for the automaton, the Store will always accept the automaton and respond with the following message (if the email address is also provided), which indicates that once the containment relation and the equivalence relation of the automaton to all other automata in the Store have been built later in the background, a notification will be sent to the user. If the automaton is actually equivalent to some equivalence class in the Store, it will be merged into the equivalence class and may be discarded if the automaton is larger than the 3 smallest automata in the equivalence class.
If the user provides an equivalent formula for the automaton, several steps
are performed to ensure the correctness and the compactness of the Store.
Assume the formula is f and the automaton is A.
-
Find in the Store a formula
gthat is syntactically equivalent tofup to propositions renaming. - If
gis found, do the following steps.-
Rename the propositions in
Aand obtainA' -
Test if
A' is equivalent to the smallest automaton forgup to propositions renaming. The upload fails if the test fails and the response message may look like: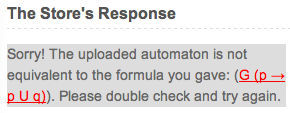
-
Test if
A' is isomorphic to one of the 3 smallest automaton forg. The upload fails if the test succeeds and the response message may look like: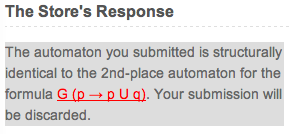
-
Test if
A' is smaller than one of the 3 smallest automata forg. The upload fails if the test fails and the response message may look like:
-
Insert
A' to the database. The response message to a successful upload may look like:
-
Rename the propositions in
-
If
gis not found, do the following steps.-
Test if
Ais equivalent tof. The upload fails if the test fails. -
Insert
Ato the database.
-
Test if
Once the upload succeeds, an image file for the automaton will be generated automatically and the Promela code of the automaton will be generated if the automaton is a Büchi automaton.
While the search for an existing formula that is equivalent to the formula to be uploaded is performed in a syntactical way (as mentioned earlier in this section), there is a background process that determines semantically the containment relation and the equivalence relation between automata in the Store. Once an equivalence class is found to be equivalent to another equivalence class, the automata and the formulae of the two classes will be merged. Emails may be sent to notify the authors of such changes.
Settings
This page provides options for the user to customize the view of the Store. The Store provides three formats for displaying QPTL formulae. Unicode characters are used in the default format. Note that versions of GOAL up to 2012-04-09 cannot parse QPTL formulae with unicode characters.
Use Cases
- Linear-time model checking: You may shop in the Store for Büchi automata that are equivalent (with probable propositions renaming) to the negations of the temporal formulae you want to verify. The automata may be downloaded in the Promela format for model checking using Spin.
- Benchmark cases for evaluating translation algorithms: Büchi Store has a substantial collection of automata with their equivalent temporal formulae; in particular, it includes automata for the LTL formulae in Spec Patterns and their negations. A subset of the collection may serve as a set of benchmark cases for evaluating translation algorithms.
- Classification of temporal formulae: The look of a temporal formula may not tell immediately to which class it belongs in the Temporal Hierarchy. You may want to practice on a few cases that do not involve going through complicated operations on automata. For example, G p ∨ G q is a safety formula because it is equivalent to G(H p ∨ H q) in the canonical safety form. Another formula G(p → F q) is a recurrence formula because it is equivalent to GF(¬ p B q).
- Reverse lookup of temporal formulae from automata: The option of uploading an automaton without giving a temporal formula may be used to find temporal formulae that are equivalent to a given automaton if some equivalent automaton with temporal formulae is present in the Store. There is no guarantee of success, however.
- Synthesis: Suppose you use the quantitative synthesis tool QUASY, which takes as qualitative specifications deterministic parity automata in GFF. You may shop in the Store for the deterministic parity automata that are equivalent (with probable propositions renaming) to the temporal formulae to be satisfied by the system, rename propositions properly perhaps with the help of the GOAL tool, and then perform the synthesis.
- Tool Integration: Suppose you want your model checker to verify that a system satisfies the temporal formula G(request → F response). Instead of using a translation algorithm, you may program your model checker to request equivalent automata from Büchi Store, which comes with Web APIs described later. The Store contains automata equivalent to G(p → F q) and will automatically rename the propositions of these automata so that the returned automata are exactly equivalent to the required formula.
API
Some public APIs are provided for accessing the contents of Büchi Store. These APIs can be accessed by visiting specific URLs. The returned values of the APIs are in the JSON (JavaScript Object Notation) format. In the following, capital words enclosed by braces are necessary parameters provided by the user, while capital words enclosed by brackets are optional parameters.
Note that when specifying a formula in a URL, "/\" and "\/" cannot be used as conjunctions and disjunctions respectively because the slash "/" has a special meaning in the URL. Please use "&", "&&", or "∧" for conjunctions and use "|", "||", or "∨" for disjunctions.
Search
-
API:
http://buchi.im.ntu.edu.tw/index.php/api/search/{FORMULA}/[TYPE] -
Description: Search for automata of type [TYPE] that are equivalent to a
formula {FORMULA}.
The automaton type can be an integer from 1 to 14 or an abbreviation
such as NBW:
- 1 for nondeterministic Büchi automata (NBW)
- 2 for deterministic Büchi automata (DBW)
- 3 for nondeterministic generalized Büchi automata (NGBW)
- 4 for deterministic generalized Büchi automata (DGBW)
- 5 for nondeterministic co-Büchi automata (NCW)
- 6 for deterministic co-Büchi automata (DCW)
- 7 for nondeterministic Muller automata (NMW)
- 8 for deterministic Muller automata (DMW)
- 9 for nondeterministic Rabin automata (NRW)
- 10 for deterministic Rabin automata (DRW)
- 11 for nondeterministic Streett automata (NSW)
- 12 for deterministic Streett automata (DSW)
- 13 for nondeterministic parity automata (NPW)
- 14 for deterministic parity automata (DPW)
-
Returned Value: an object in the following JSON format.
{ "formula" : FORMULA, "automata" : [ { "rank" : RANK, "author" : AUTHOR, "type" : TYPE, "gff" : GFF, "promela" : PROMELA }, ... ] } -
Example: The URL
http://buchi.im.ntu.edu.tw/index.php/api/search/[](req-><>ack)/DPW
returns the following object where the GFF part is omitted.
{ "formula" : "[] (req --> <> ack)", "automata" : [ { "rank" : 1, "author" : "GOAL", "type" : "DPW", "gff": "", "promela" : null}, { "rank" : 2, "author" : "GOAL", "type" : "DPW", "gff" : "", "promela" : null } ] }
Prompt
-
API:
http://buchi.im.ntu.edu.tw/index.php/api/prompt/{TERM} - Description: Find in the Store formulae that can match a search term {TERM} up to propositions renaming. The format of the returned formulae depends on the user's settings.
-
Returned Value: An array of objects in the following JSON format:
[ { "formula" : FORMULA }, ... ]where FORMULA is a formula that can match the search term up to propositions renaming. -
Example: The URL
http://buchi.im.ntu.edu.tw/index.php/api/prompt/[](req-->
returns the following array:
[ { "formula" : "[] (p --> () p)" }, { "formula" : "[] (p --> <-> q)" }, { "formula" : "[] (p --> <> q)" }, { "formula" : "[] (p --> [] p)" }, { "formula" : "[] (p --> [] q)" }, { "formula" : "[] (q --> <-> p)" }, { "formula" : "~ [] (p --> () p)" }, { "formula" : "~ [] (p --> <-> q)" }, { "formula" : "~ [] (p --> <> q)" }, { "formula" : "~ [] (p --> [] p)" } ]
Contact Us
Büchi Store is currently maintained by the same team that develops the GOAL tool. To report problems in accessing the Store or to make any other suggestions, please send emails to the following address.