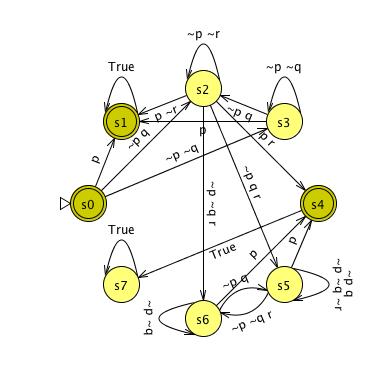
F p ∧ (¬ q ∨ p ∨ X (¬ r W (p ∧ ¬ r))) W (p ∧ (¬ q ∨ p ∨ X (¬ r W (p ∧ ¬ r))))
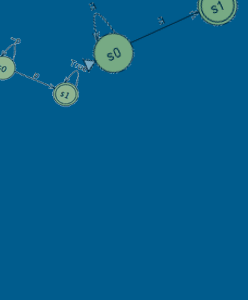
Deterministic Büchi — {s0, s1, s4}
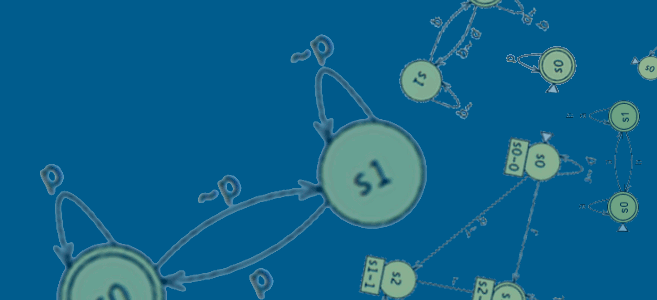
Büchi Store is an open repository of Büchi automata and other types of ω-automata. In particular, the repository contains a large collection of Büchi automata and their complements for common specification patterns and interesting temporal formulae. Different temporal formulae may specify the same ω-regular language. For a particular ω-regular language, only the three smallest Büchi automata known to the Store are kept. Some of these automata may be smaller than the corresponding ones that are generated by an automata-based model checker such as SPIN. These smaller automata could be adopted instead when using the model checker, as smaller specification automata often help in speeding up the model-checking process. Aside from the initial collection supplied by its maintenance team, the Store relies on the user to enrich the repository by uploading automata that define new languages or are smaller than existing equivalent ones. Such a repository of Büchi automata should also be useful as benchmark cases for researching translation or complementation algorithms and as pedagogical examples for teaching and learning Büchi automata and temporal logic. These apply analogously for other types of ω-automata, including deterministic Büchi and deterministic parity automata, which are also collected in the repository. For instance, the deterministic parity automata in the repository can be useful for reducing the complexity of automatic synthesis of reactive systems from temporal specifications. We hope that you will find the Store useful and appreciate your probable contributions.
To cite this work, please use one of the following:
Y.-K. Tsay, M.-H. Tsai, J.-S. Chang, Y.-W. Chang, and C.-S. Liu. Büchi Store: An Open Repository of ω-Automata. International Journal on Software Tools for Technology Transfer, 15(2):109-123, 2013.
Y.-K. Tsay, M.-H. Tsai, J.-S. Chang, and Y.-W. Chang. Büchi Store: An Open Repository of Büchi Automata. In Proceedings of the 17th International Conference on Tools and Algorithms for the Construction and Analysis of Systems (TACAS '11), LNCS 6605, 262-266, Springer, March/April, 2011.
Thank you!
Historical Notes
Büchi automata are finite automata operating on infinite words. A Büchi automaton accepts an infinite word if it induces a run of the automaton that visits some accept state infinitely many times. The formalism was invented by Büchi around 1960 to prove the decidability of the Monadic Second Order Theory of Natural Numbers [1]. Near two decades later, they found practical applications in linear time model checking. In an appendix of his seminal FOCS 1977 paper [2] which introduced temporal logic to computer science, Pnueli suggested two ways to prove the decidability of essentially the linear-time model-checking problem. (The result was originally stated as "the validity of an arbitrary tense formula over a finite state system is decidable." In the paper, only two tense (temporal) operators F (eventually or sometime) and G (always) were considered.) One proof went via the translation of a temporal formula into a Büchi automaton and then invoked the decidability of language containment between two Büchi automata, one representing the system and the other the temporal formula whose validity over the system is to be checked. This proof was a precursor to the automata-theoretic approach to linear-time model checking eloquently advocated by Vardi and Wolper in [3].
- J. R. Büchi. On a decision method in restricted second order arithmetic. In Proceedings of the International Congress on Logic, Method, and Philosophy of Science, pages 1-12. Stanford University Press, 1962.
- A. Pnueli. The temporal logic of programs. In Proceedings of the 18th Annual Symposium on Foundations of Computer Science, pages 46-57, 1977.
- M. Y. Vardi and P. Wolper. An automata-theoretic approach to automatic program verication. In Proceedings of the First Annual IEEE Symposium on Logic in Computer Science, pages 322-331, Cambridge, June 1986.